Problem - P. Perfetti (Italy)
Prove
\[\int_1^\infty\frac{\ln\left(x^4-2x^2+2\right)}{x\sqrt{x^2-1}}\,\mathrm dx=\pi\ln(2+\sqrt{2}).\]Solution
Call the stated integral $I$ and let $x=\sqrt{u+1}$, so $\mathrm dx=\frac{\mathrm du}{2\sqrt{u+1}}$ and
\[I=\frac{1}{2}\int_0^\infty\frac{\ln(u^2+1)}{(u+1)\sqrt{u}}\,\mathrm du.\]Now we let $\alpha\geq0$ and generalize the resulting integral to
\[I(\alpha)=\frac{1}{2}\int_0^\infty\frac{\ln(\alpha x^2+1)}{(x+1)\sqrt{x}}\,\mathrm dx,\]so that $I(0)=0$ and $I(1)=I$. Then differentiating under the integral sign gives
\[\begin{align*} I'(\alpha)=\frac{1}{2}\int_0^\infty\frac{x^{3/2}}{(x+1)(\alpha x^2+1)}\,\mathrm dx.\end{align*}\]We now focus on evaluating $I’(\alpha)$ by contour integration. To allow for an easier analysis we further restrict $\alpha>0$. Consider the contour integral
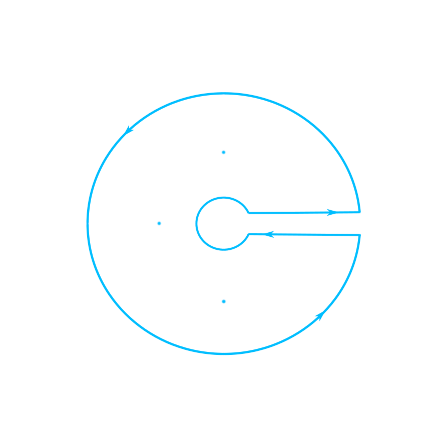
\[\begin{align} \frac{1}{2}\oint_{C_{R,\,\epsilon}}\frac{z\cdot z^{1/2}}{(z+1)(\alpha z^2+1)}\,\mathrm dz\tag{1}\end{align}\]where $R>\text{max}\lbrace1,\,1/\sqrt{\alpha}\rbrace$, $0<\epsilon<\text{min}\lbrace1,\,1/\sqrt{\alpha}\rbrace$, and $C_{R,\,\epsilon}$ is the following keyhole contour (here the branch cut for $z^{1/2}$ is on the real axis) in the following diagram.
We can evaluate $I’(\alpha)$ by calculating $(1)$ in two ways. First, by the residue theorem, the integral $(1)$ is equal to
\[\begin{align} \underset{\phi\in\left\{-1,\,\frac{1}{\sqrt{\alpha}},\,-\frac{1}{\sqrt{\alpha}}\right\}}{2\pi i\sum} \underset{z=\phi}{\text{Res}}\left(\frac{z\cdot z^{1/2}}{2(z+1)(\alpha z^2+1)}\right)=\frac{\pi}{\sqrt{2}}\cdot\frac{\alpha^{-3/4}-\alpha^{-1/4}}{1+\alpha}+\frac{\pi}{1+\alpha}.\tag{2}\end{align}\]The second evaluation of $(1)$ can be made by breaking up $C_{R,\,\epsilon}$ as
\[\oint_{C_{R,\,\epsilon}}=\int_{L_1}+\int_{\Gamma_R}+\int_{L_2}+\int_{\gamma_\epsilon}\]and examining how each integral behaves under the limit as $R\to\infty$ and $\epsilon\to0$. Along the straight path $L_1$ above the real axis we have
\[\begin{align*} \lim_{R\to\infty}\lim_{\epsilon\to0}\int_{L_1}\frac{z\cdot z^{1/2}}{2(z+1)(\alpha z^2+1)}\,\mathrm dz &= \lim_{R\to\infty}\lim_{\epsilon\to0} \int_\epsilon^R\frac{x^{3/2}}{2(x+1)(\alpha x^2+1)}\,\mathrm dx \\ &= I'(\alpha). \\\end{align*}\]We may bound the integral along $\Gamma_R$ as
\[\begin{align*} \left|\int_{\Gamma_R}\frac{z\cdot z^{1/2}}{2(z+1)(\alpha z^2+1)}\,\mathrm dz\right| &= \left|\frac{iR^{3/2}}{2}\int_0^{2\pi}\frac{e^{3i\theta/2}}{(Re^{i\theta}+1)(\alpha R^2e^{2i\theta}+1)}\,\mathrm d\theta\right| \\ &\leq \frac{R^{3/2}}{2}\int_0^{2\pi}\left|\frac{1}{(Re^{i\theta}+1)(\alpha R^2e^{2i\theta}+1)}\right|\,\mathrm d\theta \\ &\leq \frac{R^{3/2}}{2}\int_0^{2\pi}\left|\frac{1}{(R-1)(\alpha R^2-1)}\right|\,\mathrm d\theta, \\ &\qquad\text{by the reverse triangle inequality} \\ &= \frac{\pi R^{3/2}}{(R-1)(\alpha R^2-1)}. \\\end{align*}\]So we have
\[\begin{align*} \lim_{R\to\infty}\left|\int_{\Gamma_R}\frac{z\cdot z^{1/2}}{2(z+1)(\alpha z^2+1)}\,\mathrm dz\right| &\leq \lim_{R\to\infty}\frac{\pi R^{3/2}}{(R-1)(\alpha R^2-1)} \\ &=0,\end{align*}\]which implies
\[\lim_{R\to\infty}\int_{\Gamma_R}\frac{z\cdot z^{1/2}}{2(z+1)(\alpha z^2+1)}\,\mathrm dz=0.\]The integral along the straight path $L_2$ below the real axis may be evaluated as
\[\begin{align*} \lim_{R\to\infty}\lim_{\epsilon\to0}\int_{L_2}\frac{z\cdot z^{1/2}}{2(z+1)(\alpha z^2+1)}\,\mathrm dz &= \lim_{R\to\infty}\lim_{\epsilon\to0}\int_R^\epsilon \frac{e^{i\pi}x^{3/2}}{2(x+1)(\alpha x^2+1)}\,\mathrm dx \\ &= \lim_{R\to\infty}\lim_{\epsilon\to0}\int_\epsilon^R \frac{x^{3/2}}{2(x+1)(\alpha x^2+1)}\,\mathrm dx \\ &= I'(\alpha).\end{align*}\]Bounding the integral along $\gamma_\epsilon$ follows the same procedure as done for $\Gamma_R$. We find that
\[\begin{align*} \lim_{\epsilon\to0}\left|\int_{\gamma_\epsilon}\frac{z\cdot z^{1/2}}{2(z+1)(\alpha z^2+1)}\,\mathrm dz\right| &\leq \lim_{\epsilon\to0}\frac{\pi \epsilon^{3/2}}{(\epsilon-1)(\alpha \epsilon^2-1)} \\ &=0,\end{align*}\]which implies
\[\lim_{\epsilon\to0}\int_{\gamma_\epsilon}\frac{z\cdot z^{1/2}}{2(z+1)(\alpha z^2+1)}\,\mathrm dz=0.\]Combining these results shows
\[\begin{align} \lim_{R\to\infty}\lim_{\epsilon\to0} \frac{1}{2}\oint_{C_{R,\,\epsilon}}\frac{z\cdot z^{1/2}}{(z+1)(\alpha z^2+1)}\,\mathrm dz &= 2I'(\alpha).\tag{3}\end{align}\]Making an equality between $(2)$ and $(3)$ gives
\[\begin{align*} I'(\alpha) &= \frac{\pi}{2\sqrt{2}}\cdot\frac{\alpha^{-3/4}-\alpha^{-1/4}}{1+\alpha}+\frac{\pi}{2}\cdot\frac{1}{1+\alpha},\qquad\text{for }\alpha>0.\end{align*}\]Then, by the way we conveniently placed $\alpha$ in the definition of $I(\alpha)$, we have
\[\begin{align*} I &= I(1)-I(0) \\ &= \int_0^1 I'(\alpha)\,\mathrm d\alpha \\ &= \frac{\pi}{2\sqrt{2}}\int_0^1\frac{\alpha^{-3/4}-\alpha^{-1/4}}{1+\alpha}\,\mathrm d\alpha+\frac{\pi}{2}\int_0^1\frac{1}{1+\alpha}\,\mathrm d\alpha \\ &= \pi\sqrt{2}\int_0^1\frac{\alpha^{-3/4}-\alpha^{-1/4}}{1+\alpha}\,\mathrm d\alpha+\frac{\pi}{2}\ln(2) \\ &= \pi\sqrt{2}\int_0^1\frac{1-u^2}{1+u^4}\,\mathrm du+\frac{\pi}{2}\ln(2),\qquad \alpha=u^4.\end{align*}\]We can then compute the antiderivative of this last integral as
\[\begin{align*} \int\frac{1-x^2}{1+x^4}\,\mathrm dx &= \frac{1}{2\sqrt{2}}\int\frac{2x+\sqrt{2}}{x^2+\sqrt{2}x+1}\,\mathrm dx-\frac{1}{2\sqrt{2}}\int\frac{-2x+\sqrt{2}}{-x^2+\sqrt{2}x-1}\,\mathrm dx, \\ &\qquad\text{then let }u_1=x^2+\sqrt{2}x+1\text{ in the first integral and } \\ &\qquad\text{let }u_2=-x^2+\sqrt{2}x-1\text{ in the second integral to get} \\ &= \frac{\ln(|u_1|)-\ln(|u_2|)}{2\sqrt{2}}+C \\ &= \frac{\ln(|x^2+\sqrt{2}x+1|)-\ln(|-x^2+\sqrt{2}x-1|)}{2\sqrt{2}}+C.\end{align*}\]So
\[\begin{align*} I &= \pi\sqrt{2}\left[\frac{\ln(|x^2+\sqrt{2}x+1|)-\ln(|-x^2+\sqrt{2}x-1|)}{2\sqrt{2}}\right]\Bigg\vert_0^1+\frac{\pi}{2}\ln(2) \\ &= \pi\sqrt{2}\cdot\frac{\ln(3+2\sqrt{2})}{2\sqrt{2}}+\frac{\pi}{2}\ln(2) \\ &= \pi\ln\left(\sqrt{2}\cdot\sqrt{3+2\sqrt{2}}\right) \\ &= \pi\ln\left(\sqrt{6+4\sqrt{2}}\right).\end{align*}\]Denesting the radical gives
\[\int_1^\infty\frac{\ln\left(x^4-2x^2+2\right)}{x\sqrt{x^2-1}}\,\mathrm dx=\pi\ln(2+\sqrt{2})\]as desired.