Elliptic curves are a serious topic of study in pure mathematics, they are at the forefront of modern research in number theory, and they have been used to great effect in cryptographic systems. But what’s more important than any of these things is that you can use them to create hopeless problems and let them loose online. A particularly infamous problem that has circulated the internet for a few years now is the following,
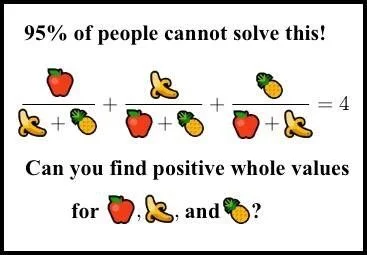
which was created in response to the multitude of poorly posed algebra emoji problems that were already out there. The key difference between the above problem and many of the others is that the difficulty clearly does not result from intentional ambiguity. Instead, this has the flavor of a prototypical number theoretic problem—easy to grasp, but totally intractable with naive methods.
Solution sketch
The essential idea behind the solution method is to recognise that the equation
\[\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}=4\]is a projective cubic curve with a rational point, which means it is an elliptic curve. To clarify,
- Projective: If the point $(a,\,b,\,c)$ is on the curve, then so is $(ka,\,kb,\,kc)$ for any $k\neq0$.
- Cubic: Can be rearranged to get a third degree polynomial $p(a,\,b,\,c)=0.$
- Has a rational point: $(a,\,b,\,c)=(1,\,-1,\,-1)$
Knowing this, we may hunt for a map $\phi$ between our cubic $p(a,\,b,\,c)$ and an elliptic curve $E/\mathbb{Q}:\,y^2+a_1xy+a_3y=x^3+a_2x^2+a_4x+a_6$ in Weierstrass form.
\[p(a,\,b,\,c)\overset{\phi}{\longrightarrow} E\]We can then do all of the tough work on $E$ in order to find a point $P\in E$ such that $\phi^{-1}(P)$ is a solution of the type we care about to $p(a,\,b,\,c)$.
Implementation with Sagemath
Sage is a powerful mathematical tool based on python that offers a way to manipulate various computationally complex objects like rings, fields, modular forms, and algebraic curves—with it we can make short work of this problem.
To start, we specify that we’d like to work over the polynomial ring $\mathbb{Q}[a,\,b,\,c]$ and we define $p(a,\,b,\,c)$ as proj_cubic.
1
2
3
4
5
6
R.<a, b, c> = PolynomialRing(QQ)
n = 4
#Define the projective cubic and put it into a form that can be transformed into a more standard elliptic curve.
proj_cubic = a*(a+c)*(a+b)+b*(b+c)*(a+b)+c*(b+c)*(a+c)-n*(b+c)*(a+c)*(a+b)
print(proj_cubic)
This gives us a^3 - 3*a^2*b - 3*a*b^2 + b^3 - 3*a^2*c - 5*a*b*c - 3*b^2*c - 3*a*c^2 - 3*b*c^2 + c^3.
Now we can use the rational point and the elliptic curve constructor to find $E$, $\phi$, and $\phi^{-1}$.
1
2
3
4
5
6
7
8
#Construct an elliptic curve the cubic curve and find the morphism and inverse morphism.
some_point = [1, -1, -1]
phi = EllipticCurve_from_cubic(proj_cubic, some_point, morphism = True)
print(phi)
phi_inverse = phi.inverse()
print(phi_inverse)
E = phi.codomain()
print(E)
This tells us the following three facts:
\[E/\mathbb{Q}:\,y^2+xy=x^3+69x^2+1365x+8281,\] \[(a\,:\,b\,:\,c)\overset{\phi}{\mapsto}(-a-c\,:\,a\,:\,6a/91-b/91+6c/91),\]and
\[(x\,:\,y\,:\,z)\overset{\phi^{-1}}{\mapsto}(y\,:\,-6x-91z\,:\,-x-y).\]This map will let us easily hunt for some point $Q\in E$ to repeatedly add to itself in hope that there is some $m$ such that $\phi^{-1}(mQ)$ is a solution to $p(a,\,b,\,c)=0$ with $a,\,b,\,c$ all positive.
1
2
3
4
5
6
7
#Find a point Q to iterate over.
try:
Q = E.gen(0); Q
except:
print(f"Solution not found for n={n}.")
print(Q)
results in (-725/4 : 7105/8 : 1) as our point $Q$.
One more short snippet of code lets us try to find a suitible $mQ$,
1
2
3
4
5
6
7
iterate = Q
while True:
iterate += Q
iterate_pc = phi_inverse(iterate) #Gives the point on the projective cubic.
if (iterate_pc[0]>0 and iterate_pc[1]>0 and iterate_pc[2]>0):
break
print(iterate_pc)
yields the terrifying looking point (154476802108746166441951315019919837485664325669565431700026634898253202035277999/36875131794129999827197811565225474825492979968971970996283137471637224634055579 : 4373612677928697257861252602371390152816537558161613618621437993378423467772036/36875131794129999827197811565225474825492979968971970996283137471637224634055579 : 1).
This does not have integer coordinates like we want, but fortunately the original curve is projective, so we can just clear the denominators and we’ll still get a solution!
1
2
3
4
5
6
7
8
9
10
#Make a, b, and c integers
d = iterate_pc[0].denom()
a, b, c = iterate_pc[0]*d, iterate_pc[1]*d, iterate_pc[2]*d
print(f"a = {a}\n\nb = {b}\n\nc = {c}")
#Test if it really works.
def test(a, b, c):
return a/(b+c)+b/(a+c)+c/(a+b)
print(f"\na/(b+c)+b/(a+c)+c/(a+b) = {test(a, b, c)}")
and this tells us
a = 154476802108746166441951315019919837485664325669565431700026634898253202035277999
b = 4373612677928697257861252602371390152816537558161613618621437993378423467772036
c = 36875131794129999827197811565225474825492979968971970996283137471637224634055579
a/(b+c)+b/(a+c)+c/(a+b) = 4
which works!
An Unusual Cubic Representation Problem
This problem, and its generalization $a/(b+c)+b/(a+c)+c/(a+b)=n$, was originally covered in a paper by A. Bremner and A. Macleod. They explore various properties of the curve, proving that there are no positive solutions when $n$ is odd, as well as showing there are solutions for an infinite familily of even $n$. Changing $n$ in the script easily gives us solutions to other variants mentioned in the paper:
n=6
a = 20260869859883222379931520298326390700152988332214525711323500132179943287700005601210288797153868533207131302477269470450828233936557
b = 1218343242702905855792264237868803223073090298310121297526752830558323845503910071851999217959704024280699759290559009162035102974023
c = 2250324022012683866886426461942494811141200084921223218461967377588564477616220767789632257358521952443049813799712386367623925971447
n=10
a = 269103113846520710198086599018316928810831097261381335767926880507079911347095440987749703663156874995907158014866846058485318408629957749519665987782327830143454337518378955846463785600977
b = 221855981602380704196804518854316541759883857932028285581812549404634844243737502744011549757448453135493556098964216532950604590733853450272184987603430882682754171300742698179931849310347
c = 4862378745380642626737318101484977637219057323564658907686653339599714454790559130946320953938197181210525554039710122136086190642013402927952831079021210585653078786813279351784906397934209
A Sum of three rationals

This problem, covered in Two More Representation Problems, can be approached using the same basic technique. Appropriately modifying the above code to account for the different curve, $n=73$, and the rational point $(0,\,0,\,1)$ yields a map to
\[E/\mathbb{Q}:\,y^2+xy+y=x^3-591594x+175089846\]and the solution
a = 5516052940379835723918624062995170304792670702
b = 723869051938634952455000067289242669675739356
c = 11072099852925046330240381983962055577398063
A more monstrous problem
A similar problem is:

By using a suprisingly simple recurrence, starting with a point found by Noam Elkies, it can be shown that the smallest solution in the positive integers has coordinates upwards of $10^{21388}$. This problem is dangerous!
Tips for running Sage
The recommended approaches to running Sage were not working for me, but the following tricks helped (assuming you already have python and jupyter notebooks installed):
In WSL, run the following 3 commands:
1
2
3
sudo apt update
sudo apt-get upgrade
sudo apt-get install sagemath
You can then enter sage -n jupyter in WSL to start a notebook. Lastly, go to localhost:8888 in your browser and start a new notebook file.